This blog post is going to introduce what QFT is about, then move on to one of the simplest fields - the Klein-Gordon Field, a real scalar field - and the quantization of that field. The next posts in the series will get into various other topics, but will more than likely cover things like: the Dirac Equation and the quantization of spinor fields related to the Dirac Equation; Lie Groups and the geometry of the local gauge invariance found in Quantum Electrodynamics (QED) - the field theory for explaining the Electromagnetic Force; field Lagrangians based off a more general gauge invariance, or non-Abelian symmetry groups, like the Yang-Mills Lagrangian found in Quantum Chromodynamics (QCD, the strong force). If some of the physics jargon in this paragraph doesn't make sense, don't worry - it should become more clear through the discussions.
Natural Units
Before we dig into things, let's go over a concept that comes up everywhere in QFT and Relativity - Natural Units.
Despite the plethora of crazy units out there, there are really only 3 basic units: mass (M), length (L), time (T). All other quantities can be written in terms of these three basic units. For example, force is expressed in terms of the three basic units, as follows.
There are all sorts of man-made conventions to quantify these three basic units, like meters, inches and miles for length and kilograms and slugs for mass. However, three fundamental constants of nature allow us to get rid of all man-made system of units. Let's see how.
First, upon the advent of Special Relativity and discovery of the constancy of the speed of light (c), Einstein realized we no longer need separate units for length and time. As strange as that sounds, you're already familiar with this notion if you ever talked about light years. Sounds like a notion of time, but it is really a measure of length. In fact, because of the constancy of c, if we consistently measure time in terms of length (or vice-versa), c will not only become dimensionless, but will be equal to 1.
(Actually, what's really intriguing is not the constancy of the speed of light, but that there exists a c such that the spacetime interval is invariant under changes of inertial coordinates. This means that all observers agree upon separations in spacetime, but disagree, in general, upon separations in space and time, separately. As a result, the speed of light becomes more of a conversion factor between space and time, appearing as a fixed velocity for all observers.)
Newton's discovery of the universal law of gravity brought another constant (G) into the picture. Comparing the kinetic energy (½mv²) of a particle with mass, m, in a gravitational potential, with the potential energy (GMm/r), we find that the combination GM/c² has dimensions of length. With two universal constants now (G and c) we can effectively write mass in terms of length (or time).
Planck topped all this off with his discovery of the universal constant of Quantum Mechanics, ℏ. The Heisenberg Uncertainty principle says ℏ divided by momentum (Mc) is a length. This means we can equate the two lengths, ℏ/MC and GM/c², and find that the combination ℏc/G has the dimensions of mass squared. In other words, we can use the three fundamental constants - G, c and ℏ- to define a mass called the Planck mass.
Likewise, we can immediately define a Planck length (again with Heisenberg's help):
and, with a little more help from Einstein, a Plank time:
So, if we consistently measure mass in terms of the Planck mass, time in terms of the Planck time, and length in terms of the Planck length, we can set ℏ, G and c to 1, in an similar fashion to how we set c to 1 above. This is what is referred to as Natural Units.
Incidentally, the fact that the Planck mass is so huge is an ongoing mystery in physics and it represents the extreme feebleness of the gravitational force, relative to the other three. Also, because the Planck mass is large, the length and time are teeny.
The Planck length and time represents the scale at which physicists believe the notions of space and time may no longer apply, with some more fundamental structure to reality waiting to be discovered. The Planck time is ~5.4*10^-44 seconds and the Planck length is ~1.6*10^-33 centimeters. Both are very tiny! Also, when you hear physicists say the known laws of physics don't allow us to go all the way back to the Big Bang (t=0), the Planck length and time is the specific stopping point they are referring to. The laws of physics, as we know them today, break down past that point. We need a quantum field theory for gravity - called Quantum Gravity, for short - to go further. This is still a work in progress.
Getting back to the Natural Units, remember that all quantities can be written in terms of mass, length and time. Nature has provided us with a set of natural units to measure her by, via the three fundamental constants. Some folks like to say this suggests we have discovered all the fundamental principles of nature, but I think that is going too far. There are good reasons to suspect there is more to nature. In addition, there is gathering evidence that the three fundamental constants just mentioned may not really be constant!
Why Quantum Field Theory
Quantum Field Theory handles both the domain of the very small (Quantum Mechanics) and the very fast (Special Relativity), therefore it is somewhat of a "marriage" of those two separate theories. There are additional points that makes Quantum Field Theory important.
(1) The combination of Quantum Mechanics with Special Relativity implies that particle number is not conserved
We verify every day in particle accelerators that particles can be created and annihilated, but neither QM nor SR have the theoretical, or mathematical, framework for handling this. To further illustrate the problem consider a particle trapped in box of size L. The Heisenberg Uncertainty principle says that you cannot know both the position and momentum of a particle simultaneously with infinite precision. This is expressed mathematically as: Δp ≥ ℏ/L. In a relativistic setting, this implies an uncertainty in energy of: ΔE ≥ ℏc/L. But, when we have an uncertainty in energy equal to twice the mass of the particle (ΔE = 2mc²) we can start to pop particle antiparticle pairs out of the vacuum, because in relativity we have a mass-energy equivalence. In other words, if you try to pin down a particle's position too far, you can no longer guarantee you are working with just one particle. The lower limit on how well a particular particle can be localized is called the Compton Wavelength, defined as: λ = ℏ/mc, where m is the mass of the particle in question. This immediately tells us that any equation dealing with only a fixed number of particles is doomed to failure in the realm of the very fast and very small. The Schrodinger equation of QM is such an equation. QFT offers a way to handle regimes where particle number is no longer fixed, as we'll see later on.
This is more profound than it sounds. There are two types of elementary particles in the world: bosons (integer spin) and fermions (half-integer spin). Elementary particles are particles that are not known to have any substructure, unlike say the proton and neutron, which are thought to consist of three quarks each. It is believed that the quarks are, however, elementary particles and they are classified as fermions, like the electron, the muon, and the neutrinos. Elementary matter particles like the electron are grouped under the fermions. The force carrying particles like photons (mediator of the electromagnetic force), W and Z bosons (mediator of the weak force) and gluons (mediator of the Strong Force) are grouped under the bosons. Although a QFT for gravity has not been fully worked out, it is believed the graviton will be the mediator of that force. (The graviton is distinguished from the other fundamental bosons, in that it has Spin 2). In each case, the particle is the smallest ripple that each "force" field can come in. Therefore, the graviton is the smallest ripple spacetime - the field in gravity - would be able to come in. Weird, huh?
The important point here is that every electron is exactly like every other electron in every possible way! Within each class, or type, of particle, every particle is utterly indistinguishable from each other. Swapping two particles around will leave the existing state completely unchanged - apart from a minus sign, in the case of fermions. This minus sign makes for different statistics between the two particle types. It reflects the fact that any number of Bosons can occupy the same quantum state, but no two fermions can do the same. This is what makes chemistry (and the reality we know and love) possible, since chemistry depends on where electrons reside within specific atomic orbits, or shells, which are specific quantum states. If electrons could share the same quantum state, they could all just cascade down to the ground state, or lowest orbit of the atom, and we wouldn't have any chemical interactions! This is all related to the Pauli Exclusion principle, which you may have heard of before.
Anyhow, with QM, these statistics must be put in by hand, but they fall out of Quantum Field Theory in a very natural way, in something called the Spin-Statistics theorem.
(3) Causality
To see what Quantum Field Theory offers in the way of enforcing our common sense notions of causality, let's take a look at the amplitude for a particle to propagate from point one point to another, which is given by:
This equation is using Dirac's Bra-Ket (< | | > ) notation, which is common throughout Quantum Mechanics and is a way to represent abstract vectors (and dual vectors). In Quantum Mechanics, the state of a particle is represented by just such an abstract vector, called the state vector, which "encodes" all the statistical information for all possible observables (like spin, or position). This state vector lives in a special mathematical space called a Hilbert space, which is an infinite dimensional, square-integrable, complex vector space. Square-integrable just means the state-vector can be normalized in such a way that the probability interpretation of QM makes sense. The time evolution of the state of the particle is represented by rotations of this state vector within Hilbert Space. For each observable, the state vector can be expanded within what's called the eigenbasis for the operator representing that observable. You can think of these as axes, or dimensions, each of which represents a possible outcome upon measurement. The projection of the state vector along a specific axis, or eigenvector, quantifies the probability of obtaining that specific outcome upon measurement. To be specific, the probability is the modulus squared of the projection of the state vector along a specific eigenvector. The only possible values the projections can take are the eigenvalues of the specific eigenvectors of that operator. Despite being a complex space, these eigenvalues are guaranteed to be real (by the fact that quantum operators are Hermitian operators, which means the transpose conjugate of the matrix representing the observable is equal to the original matrix). Also, it's obvious an observable like position has an infinite number of possible outcomes, which is why Hilbert space needs to be able to accommodate an infinite number of dimensions. (If you don't need [or want!] a refresher on technical QM jargon, feel free to ignore that paragraph and the following one!)
Continuing on, the expression above is called the propagator and the exponent is the unitary time-evolution operator. A unitary matrix is one where the transpose conjugate of the matrix equals the inverse of the matrix. These are the complex-space analog of rotation matrices found in every-day normal (i.e. real) Euclidean space. In other words, a unitary matrix performs a rotation in complex space, just as orthogonal matrices perform rotations in regular space. So, the propagator takes some initial state-vector and time evolves it to some final state, by rotating it through the complex Hilbert space, via the unitary time-evolution operator, as outlined above.
Getting back to the expression above, we note that in a non-relativistic setting, E=p²/m. Inserting a complete set of momentum states and performing the integral, ultimately gives:
The only thing important to note here for our purposes is that this expression is non-zero for all x and t, which means that a particle can propagate between any two points in an arbitrarily short amount of time. It doesn't get better when using the relativistic expression for E, or energy. This is a clear violation of causality in a relativistic theory, because it would allow for faster-than-light signal propagation. This is bad news in relativity because, if propagation speeds greater than the speed of light are allowed, a reference frame can always be found where the effect proceeds the cause (e.g. you arrive back home, before ever leaving!). To preserve sanity in the Universe, we like to avoid situations like this.
QFT solves this causality problem one finds in QM (under a relativistic setting) in a rather amazing way - it postulates the existence of anti-particles! Even in QFT, the amplitude for a particle to leak outside the light cone (i.e. faster than light propagation) is small, but non-zero. But, this amplitude is canceled exactly by the amplitude of the particle's corresponding anti-particle. QFT solves the causality problem by introducing anti-particles, or rather nature contains anti-particles to preserve sanity in the Universe!
Klein-Gordon Field
Before we dig into the Klein-Gordon equation and corresponding fields, we need to quickly derive the Euler-Lagrange equation for a field. This equation is useful for obtaining the equations of motion for a system from its Lagrangian. Although Lagrangians come in all sorts of complicated scary looking forms, they basically boil down to kinetic energy minus potential energy. The Lagrangian is a kind of "global" summary of the dynamics of the system and is a very useful expression in Quantum Field Theory for several reasons.
Symmetries and their associated conversation laws play a central role in QFT and these are handled most efficiently within the Lagrangian formulation. As we'll see below, the Klein-Gordon field we'll be investigating is a free field, which means that particles don't interact with each other. It's by adding non-linear terms to the Lagrangian that give rise to particle interactions. There is also an area of study in QFT called the renormalization group, where one can investigate the parameter space of all possible Lagrangians to show that whatever form the unknown theory at higher energies takes (remember, from above, that QFT is valid only up to some value of momentum/energy), it should reduce to what's called a renormalizable field theory. Renormalizable means we can handle the nasty infinities we talked about above, which rear their ugly heads everywhere in QFT. So, basically, the Lagrangian formulation is very insightful and useful in QFT and, therefore, is the preferred way to go. If you don't like looking at Lagrangians, you're going to hate Quantum Field Theory!
A fundamental quantity in classical mechanics is the Action (S), which is the time integral of the Lagrangian (L). The Lagrangian approach to classical mechanics is a global approach in that it tries to determine the entire trajectory of a particle in one stroke, rather than concern itself with infinitesimal time variations like in the Newtonian Approach. The Action for a field is given by the following formula. Since we are working with fields, notice that our dynamical variable in these equations is the field (φ). In Quantum Field Theory, position, which is normally a dynamical variable in classical mechanics, gets demoted to a mere label, similar to time. The field itself becomes the prime dynamical variable in QFT. Note also that we are working with the 4 dimensions of spacetime, as well.
The cursive L is the Lagrangian density, or the spatial density part of the total Lagrangian. Note that S is a functional. Whereas a function takes a variable as its argument and returns a number, a functional takes a function as its argument and returns a number. Hamilton's Principle of Least Action says that when a system evolves from one configuration to another, it does so along the path of least action, or an extremum of S. This is one of those mysterious facets of nature. Why does nature behave this way? Nobody truly knows.
If we vary S and set the first-order contributions to zero, this will give us an extremum of S and provide us with an expression for the equation of motion for the system in question. The first-order changes in the Action are given by the next equation.
We need to pull a δφ out of the second term in brackets, so that we can factor it outside the brackets along with the one on the first term. This is accomplished by integrating the second term by parts, leaving us with:
In order for this to vanish for any arbitrary change in the field (φ), the expression in the brackets must vanish, leaving us with the Euler-Lagrange equation, in this case for a field.
Now, let's consider the following Lagrangian for a real scalar field, or our Klein-Gordon field.
Where we are using the Minkowski metric of Special Relativity, defined by:
It's not too uncommon to see the minus signs swapped around, but as long as one is consistent it all works out.
Let's now plug this into the Euler-Lagrange equation. Taking the derivative with respect to the field (φ) is straightforward giving us a (-m²φ) term. The second term is a bit trickier because it requires managing the indices a little bit. It goes like the following.
Plugging into the Euler Lagrange equation, we get the following:
This is the Klein-Gordon equation, which is the equation of motion for a real scalar field. Again, note that the prime dynamical variable in this equation of motion is the field.
Quantizing the Klein-Gordon Field
Everything we have done so far is still for a classical field. Ultimately, to handle the creation and annihilation of particles and the interactions between the particles of the field, we want a quantum field. After all, a particle is the smallest "ripple", or the smallest "quantum", that a particular field comes in!
Before we take a look at how to quantize the Klein-Gordon field, it will first help to review a simpler problem from Quantum Mechanics - the harmonic oscillator. After seeing how to quantize the harmonic oscillator, we'll proceed unto the more complicated, but analogous, procedure for quantizing the Klein-Gordon field.
You can think of the harmonic oscillator as the quantum version of a classical spring, which is the type we're all familiar with. As you picture some spring bobbing up and down, you know it can have any old energy, or it's energy spectrum is continuous. However, for a quantum string the energy states are discrete, with energies in between being forbidden. In other words, you'll never see a quantum spring take on those energies. (Of course, on a fundamental level even classical springs are dictated by the laws of quantum mechanics, but on a macroscopic scale the discrete nature of quantum mechanics appears continuous. It's only by "zooming" way in ... wayyyyy, way in ... that they become obvious)
We need to start off with the Hamiltonian for the Quantum Harmonic Oscillator.
where p and q are momentum and (generalized) position, respectively, and omega is the frequency. The Hamiltonian is basically the total energy of the system, or kinetic energy plus potential energy. What we need to do is find the spectrum of this Hamiltonian, or the allowed energy values that the quantum system can take.
What's usually done now is to introduce what are called ladder operators in QM. Ladder operators step up, or step down, all the allowed energy values for the system in question. We'll see below that there are analogous operators in QFT called creation and annihilation operators that create and annihilate particles. This was what we were looking for above when we mentioned that particle number is not conserved. These operators will give us the flexibility to handle the creation and annihilation of particles. For a very rough analogy, you can imagine a field as a mattress made of springs stretched out through space. These springs can take on some minimum energy value, which represents a particle, or the smallest allowed ripple/wave of that field.
Here are the ladder operators for the QM version of the harmonic oscillator:
These equations can be reversed to find q and p, in terms of the ladder operators, as follows.
In QM, one encounters something called the commutator, which goes like [a,b] = ab - ba. The commutator for the ladder operators is:
The relation is important, because we'll also have similar (but more complicated) expressions for the creation/annihilation operators in QFT. Putting this commutation relation to use, we can rewrite the Hamiltonian in terms of them.
We can also show that the commutator of the Hamiltonian with each ladder operator gives the following.
Now, by acting on the energy eigenkets (|E>) and using the commutation relations we have established so far, we can see that the ladder operators step up and down in energy in steps of omega. (We also use the Schrodinger Equation in the following abstract form H |E> = E |E>.)
It may not be obvious but we have found the spectrum of allowed energy states for the quantum harmonic oscillator.
These are the discrete energies our "spring" is allowed to have. Normally, this is bounded from below by a ground state, like in the quantum harmonic oscillator, but we won't cover that here. I just wanted to introduce the concept of ladder operators, or creation/annihilation operators in this more simple form, before moving on to the more complicated looking QFT operators.
Let's take a look at those now and begin quantizing the Klein-Gordon field. First, we note that the general solution to the Klein Gordon equation is the following:
You can check this by plugging it back into the Klein-Gordon equation and make sure things work out. Also, this solution was fixed to ensure that it is always a real value. In analogy with the equation for p in the quantum harmonic oscillator, we write our conjugate momentum, as follows:
The creation and annihilation operators for our Klein-Gordon field are analogous to the ones for the quantum harmonic oscillator above and given here:
Now that we have the commutation relations between the creation and annihilation operators, let's work out just one of the commutation relations for the field and its conjugate momentum, so we can see how the math goes.
The second line writes out the commutation relation. Note how we used p to label the momentum for the field term and q to label the momentum for the conjugate momenta term. The labels are arbitrary, but they must be different for things to make sense. A few steps are skipped, but after multiplying all the terms out they can be grouped up via the commutation relations for the creation and annihilation operators. The first and last commutator vanish, by our first proposed commutation relation stated above. The second and third commutator can be reduced to three dimensional Dirac delta functions by the second commutation relation, as follows:
Performing the q-integral will basically turn all the q's in the exponents to p's, per the usual behavior of a dirac delta function under an integral. This gives the following.
Using the standard integral formula for Dirac delta functions and the fact that a constant can be pulled outside a Dirac delta function by multiplying by the inverse of the absolute value of that constant, gives the final result above. This basically says the commutator is equal to i, if x is equal to y, and otherwise vanishes.
Now, the formula for the Hamiltonian of a field, which we won't bother deriving, is
As you can see there will be very similar math to the commutation relation we just calculated above, however there is probably a couple pages of math that I don't want to put up in explicit detail. If you can work through the commutation relation above, the Hamiltonian is doable. I'm just going to quote the final result here and discuss some of the implications:
On the second line above, we simply used the commutation relations again for the creation and annihilation operators. When this second term is integrated it's going to blow up, per the usual Dirac delta function behavior. QFT is rife with infinities and this is typically the first of many that one encounters. Let's explore what's going on.
There are really two infinities hiding in that term. The first is due to that fact that we're integrating over all space and calculating total energy, when we should be going after energy density. This kind of infinity is called an infrared divergence. If we corrected that expression for energy density, we are left with a term that is a sum over all modes of the zero-point energies of the field. However, this term still blows up as p (momentum) goes to infinity. Integrating over all values of p is assuming that our theory is valid to arbitrarily high energies, but we know QFT is valid down to some minimum length scale and correspondingly to some finite momentum, or energy scale. This kind of infinity is called an ultraviolet divergence and was caused here by our own hubris.
There is a real easy way to handle this infinite term. Ignore it. In physics, it's only differences in energy from the ground state of H that can be measured, so this infinite shift in the energy density cannot be detected experimentally (as far as we know!). Therefore, we can just drop that term. Easy enough. But ... the rest of the infinities one encounters in QFT aren't quite so easy to get rid of!
There is one big caveat to dropping that term. Gravity is supposed to see everything! The sum of all the zero-point energies of the field should contribute to the stress-energy tensor in Einstein's equation for General Relativity (GR). In GR, it's not just the mass that effects gravity, but the total local energy content, which is recorded in the stress-energy tensor. This energy would show up in a term, which you have probably heard of before - the cosmological constant. For some reason, these energies either don't contribute, or cancel to a high degree of accuracy. This is known as the cosmological constant problem. If you would like a Nobel Prize, you could always try figuring that one out ;-)
So, we have successfully (and partially!) quantized a real scalar field (the Klein-Gordon field) and we have found the Hamiltonian and the creation and annihilation operators. However, you may be wondering what about the antiparticles (and causality!) For a real scalar field, each particle is it's own antiparticle. It's only when we start to consider complex fields that we will get distinct antiparticles for each particle of the field and the corresponding distinct set of creation and annihilation operators for creating/annihilating those antiparticles.
Well, I guess this post got a little heavy. I think before continuing on to the next Quantum Field Theory post, I will probably do one that's a little more fun next time. Stay tuned!


































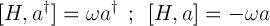
















No comments:
Post a Comment