Thought I would start off my first
physics blog with a topic I always thought was kind of neat –
cosmological red shifts. Also, when I first learned about this, I
realized how I was walking around with some mistaken notions for
quite some time and how descriptions from popular physics, or popsci,
promulgate these mistaken notions.
Before I start, I should warn this is a somewhat contentious issue and interpretation is important. I'll try to present a simple description, which will probably oversimplify the matter too much, but at least make for an entertaining blog ... I hope! I will leave links at the bottom to some professional physicists, where they duke out the matter in greater detail, for those interested. At the very least, I think you'll see the whole business of redshifts in Cosmology isn't quite as simple as popsci can make it sound at times.
Before I start, I should warn this is a somewhat contentious issue and interpretation is important. I'll try to present a simple description, which will probably oversimplify the matter too much, but at least make for an entertaining blog ... I hope! I will leave links at the bottom to some professional physicists, where they duke out the matter in greater detail, for those interested. At the very least, I think you'll see the whole business of redshifts in Cosmology isn't quite as simple as popsci can make it sound at times.
The complications arise between what we
mean by a Doppler Shift and what we mean by a Cosmological Red Shift.
They are different. But, first, let’s start with what a wave is. The easiest way to get a
feel for a wave is by imagining ones we are all familiar with –
water waves.
 |
| Water Waves |
A water wave is the propagation of
energy through water. As you can see, there are troughs and crests,
which correspond to the wave amplitude. Also, we can see that the
waves repeat. The length of one unique segment
(crest-to-trough-to-next-crest) is the wavelength. The number of
crests that pass by a fixed point in a fixed amount of time is called
the frequency of the wave. There is an inverse correspondence
between wavelength and frequency – high frequency means small
wavelength and vice versa. We can represent all this with simple
plots, like the following.
Sounds waves are the propagation of
density perturbations in air. Electromagnetic waves are the
propagation of electric and magnetic fields. Light is one kind of
electromagnetic (EM) wave, or specifically a certain frequency/wavelength range of the EM spectrum. Most waves require a medium to travel through
(like the water, or air) but electromagnetic waves can travel through
empty space. This is due to how the electric and magnetic fields
interact with each other – a time varying electric field creates a
magnetic field, and vice versa, which is very evident when looking at
Maxwell’s Equations.
Now, when a source like the horn on a
train is moving, the waves will get compressed and stretched (i.e.
their wavelength will change). In the direction of motion the wave
crests will get compressed and in the opposite direction they will
get stretched. Everybody is familiar with this by how the pitch of a
train is very high when it comes toward you, but then decreases after
it passes. This image visually depicts the waves beings stretched
and compressed.
With light, wavelength corresponds to color. Blue-ish light is higher frequency, smaller wavelength. Red-ish light is lower frequency, larger wavelength. We, therefore, say the light is red-shifted or blue-shifted by a moving source.
All this is the familiar Doppler Shift.
It comes into play in astrophysics quite often. Stars moving away
from us have their light red-shifted. Stars moving towards us have
their light blue-shifted. On a larger scale, galaxies moving away
from us have their light red-shifted. Galaxies moving towards us
have their light blue-shifted.
We may all be familiar with this from the Big Bang, which says the Universe has expanded from a small, dense region a finite time in the past. Spacetime itself was created in the Big Bang, so it is spacetime itself that is expanding. The Big Bang is actually a pun on words, because there was no “bang” that happened in some pre-existing space. In addition, our physics are only valid back to around 10^-44 seconds (called the Planck Time) and therefore the Big Bang says nothing about the actual “bang”, or moment of “creation”.
We may all be familiar with this from the Big Bang, which says the Universe has expanded from a small, dense region a finite time in the past. Spacetime itself was created in the Big Bang, so it is spacetime itself that is expanding. The Big Bang is actually a pun on words, because there was no “bang” that happened in some pre-existing space. In addition, our physics are only valid back to around 10^-44 seconds (called the Planck Time) and therefore the Big Bang says nothing about the actual “bang”, or moment of “creation”.
So, as spacetime expands, it is taking
all the galaxies along with it, similar to how flowing water sweeps
things along with it. The way it works is compared to an inflating
balloon. Using the illustration below, we can see that all points on the balloon will
view themselves as if they are at the center of expansion, just as we
do on Earth.
Therefore, we should see the light from distance galaxies predominantly redshifted. The further a galaxy is away from us the faster we will see it receding away and the more its light will be redshifted. Here’s where we get into trouble. If we think about this redshift as solely a Doppler Shift, we find that the some very distant galaxies are receding away from us at faster than the speed of light! But, we know from Special Relativity that nothing can travel through space faster than c (i.e. c = the speed of light).
What’s going on here?
Therefore, we should see the light from distance galaxies predominantly redshifted. The further a galaxy is away from us the faster we will see it receding away and the more its light will be redshifted. Here’s where we get into trouble. If we think about this redshift as solely a Doppler Shift, we find that the some very distant galaxies are receding away from us at faster than the speed of light! But, we know from Special Relativity that nothing can travel through space faster than c (i.e. c = the speed of light).
What’s going on here?
I’ll give a hint – cosmological
redshift is part of the answer!
Let’s also be more specific about what
Special Relativity (SR) says. It says nothing can move through space
faster than c, or the speed of light. It doesn’t say anything
about the expansion rate of space itself. So, even though a galaxy cannot move through space faster than c, it can be swept away by the expansion of space at faster than c. In addition, SR says
anything with mass must travel slower than c, but massless particles,
like the photon (i.e. light), must always travel at c (through a
vacuum), as viewed by any observer.
A cosmological redshift is caused by
the expansion of spacetime itself. In other words, a galaxy can
appear to have red-shifted light even if it’s not moving through
space. This effect can become predominant on cosmological (or, vast!)
distance scales.
In addition, in a curved spacetime (or,
expanding spacetime) we cannot even clearly talk about relative
velocities between two objects and, therefore, cannot clearly define
a Doppler Shift. Let’s see why.
Normally, when we add two vectors A and B in a flat space, we’ll move the tail of B to the tip of A, then
we’ll draw a new vector that goes from the tail of A to the tip of
B and this vector is then (A + B). Note that when we move B we keep
it parallel – this is called parallel transport. We can also use the parallelogram technique, which is illustrated in the next figure. Notice that the dashed line representing the top perimeter of the parallelogram is parallel to and has the same length as A, likewise with the other dashed line and B.
 |
| Vector Addition |
The problem arises when we see that
parallel transport through a curved space does not necessarily leave
you with the same vector you started out with. To make matters
worse, parallel transport is path-dependent. Depending on what path
you drag B along to get to the tip of A, you may end up with a different B and, therefore, a different answer for A + B. This can be seen in
the following images. As a vector gets parallel transported around a
curved surface of a sphere, we end up with the vector pointing in a
different direction once it is returned back to its original position. Note the difference between the red and blue arrows below.
 |
| Parallel Transport of a Vector on a Curved Surface |
The more dynamic (i.e. curved,
expanding, etc.) the space the more convoluted this becomes. Now, if
vectors A and B represent the velocities of two galaxies labeled A
and B, and the space is highly dynamic between them, we can see how
defining the relative velocity between them (A + (-B)) becomes difficult. In fact, to say a galaxy is receding away from us, which implies relative velocity, is a mathematically imprecise statement in a dynamic, curved spacetime. It's one reason why we find things receding away from us faster than the speed of light, if we think of all this solely in terms of Doppler Shifts and galaxies moving through space.
Let’s now look at two scenarios, or
thought experiments, that will illustrate further the difference
between a Doppler Shift and a Cosmological Redshift. Then, for
those of you who haven’t fallen asleep yet and are eager to see
more details, we’ll do a small mathematical derivation that will
more deeply illustrate what a Cosmological Redshift is!
For the first scenario, let's take two galaxies, labeled Galaxy A and Galaxy B, that are at rest with respect to each other, as depicted in step (i) in the image below, and have galaxy A emit a photon in the direction of Galaxy B. In step (ii), let's move the galaxies through space and bring them back to rest before the photon reaches galaxy B. (Remember, this is a thought experiment, so we can pretend to be God and hurl things around the Universe at will!) Now, when the photon reaches Galaxy B in step (iii), there will be no Doppler shift, because the galaxies are at rest during emission and absorption. Doppler shift depends on relative velocities.
For the first scenario, let's take two galaxies, labeled Galaxy A and Galaxy B, that are at rest with respect to each other, as depicted in step (i) in the image below, and have galaxy A emit a photon in the direction of Galaxy B. In step (ii), let's move the galaxies through space and bring them back to rest before the photon reaches galaxy B. (Remember, this is a thought experiment, so we can pretend to be God and hurl things around the Universe at will!) Now, when the photon reaches Galaxy B in step (iii), there will be no Doppler shift, because the galaxies are at rest during emission and absorption. Doppler shift depends on relative velocities.
 |
| No Doppler Shift (or any shift) since galaxies are at rest with respect to each other at emission and absorption |
The next scenario is very similar, except for step (ii). This time, in step (ii), we are NOT going to move the galaxies through space. Instead, we are going to expand the space between the galaxies, thereby effectively making them the same distance apart that they achieved in the previous scenario.
 |
| In this scenario, the photon experiences a redshift! |
This time, when Galaxy B detects the photon, a redshift is found! Despite the fact that steps (i) and (ii) are identical and despite the fact that all the distances are the same, the photon is redshifted in this scenario and this is solely due to the expansion of space. An expanding spacetime redshifts photons, or causes them to lose energy.
Okay, still awake? How could you not be awake and riveted at the edge of your seat at this point ;-)
Let's push on and do some math that will show this result more explicitly! What I hope to achieve in this section is to give the reader, who has a basic understanding of calculus and tensor notation, a feel for some of the concepts in Special and General Relativity and hopefully a greater appreciation for the topic of this thread. For those without the math background, there may still be some neat gems from Relativity waiting for you. Just gloss over the equations.
We'll start with what's called a simplified Robertson-Walker metric. (The full Robertson-Walker metric characterizes our actual Universe, but it is much more simple and heuristic to use this simplified one, as the end result is the same in both cases)
To get a little more familiar with the metric, think of the Pythagorean Theorem for calculating distances (x² + y² = z²). Notice how similar this is to the Robertson-Walker metric. This is all a metric does - it calculates distances. However, through Special Relativity, we have learned to treat space and time on the same footing. Einstein unified the two and so now we are talking about distances not just in space, but rather distances in spacetime! This also means we are now dealing with 4 dimensions (3 spatial, 1 time) and not the usual 3 spatial dimensions. a(t) is called the scale factor and, as you can see, it is dependent on time and has an effect on the spatial dimensions.
The little minus sign on the time part above, characterizes the signature of the metric. This minus sign is partially responsible for some of the cool features we find in Special Relativity. This is called a Lorentzian signature. If there was a plus sign there instead, we would have a 4-dimensional Euclidean metric and, other than the extra dimension, this isn't nearly as interesting! (As a side note, it is possible to transform between Lorentzian and Euclidean metrics using what's called a Wick Rotation. This is done all the time in Quantum Field Theory calculations to simplify the math)
We will now use a variational approach to calculate what are called the Christoffel Symbols (more on those below) and obtain the geodesic equation (more on that below, too) for this simplified Roberston-Walker space. We're basically going to be solving for curves of maximum proper time, which correspond to the shortest-path through a curved space, which is basically what a geodesic is. This is all somewhat similar to deriving the Euler-Lagrange equations of motion by varying the action and using Hamilton's Principle of Least Action. Anyhow, we won't derive it here, but the following formula is used, which utilizes proper time, τ, for it's parameter.
Plugging in for our specific metric, gives:
We'll drop the y and z spatial dimensions for simplicity and have used the Kronecker delta to keep things clean.
Now, let's first vary with respect to time, meaning:
and
We neglected terms that are second order, or higher, in the infinitesimal variation and we also skipped a step or two on the second line. Plugging these into our variational formula and only keeping terms that contribute to first-order changes in I, we get:
We want to solve for vanishing δI, or vanishing first-order changes in I, because this is indicative of a critical point, or point of maximum proper time, as discussed above. In order to get a reasonable, and useful, expression for when δI vanishes from the equation above, we need to get that δt out of the derivative in the first term, so that we can pull it outside of the square brackets. We can achieve this by integrating the first term by parts, ultimately giving us:
In order to make this vanish for any arbitrary δt, the expression in parentheses must vanish. This is then equivalent to the geodesic equation,
from which we can read off the Christoffel Symbols. We don't actually need to obtain all the Christoffel symbols for the problem we're tackling, but because they're interesting let's talk about them anyhow. We'll also talk about the geodesic equation, which we do need for the problem at hand.
Christoffel symbols are also called connection coefficients. Put very simply, they provide a connection between vectors that lie close to each other in a curved space. Put more technically, they provide a connection between vectors in nearby tangent spaces. The covariant derivative quantifies the instantaneous rate of change of a vector (and more generally, a tensor field) in comparison to what the vector (or, tensor) would be if it were parallel transported. The Christoffel symbols provide the connection to transport vectors from one tangent space to another and are a crucial part of the covariant derivative. All of this would be a moot point if we were in a flat space. In the limit of vanishing curvature, the Christoffel symbols also vanish and the covariant derivative becomes the regular derivative we're all familiar with in flat space.
The geodesic equation is the generalization of a straight line in curved space. In other words, a geodesic is the shortest path in curved space. If you take a look at the geodesic equation above, you'll see that when the second term vanishes as a result of the Christoffel symbols being set to zero, we are left with the equation of a straight line in flat space.
Moving on, let's set the term in parentheses, which is essentially the geodesic equation, to zero, like we said we would above and use the affine parameter, λ, instead of the proper time, τ. An affine parameter is any one that can be related to the proper time in a linear fashion (λ = a* τ + b).
This is a differential equation, which is solved by the following:
We'll use this below.
Now that we're using λ, we can take a look at a null path. Null paths are paths of zero spacetime distance and they are the paths followed by massless particles, such as photons. Let's think about what this means. First, ds² (or ds) is called the interval and it's an invariant. Although space and time are now relative, every observer will always agree on the interval between any two events. Also, recall that space and time are on the same footing in Special Relativity. This means we must now think of motion, not just through space, but through time, as well. Sitting at your monitor reading this blog, all your motion is in the time dimension with zero motion in the spatial directions. Looking at the Robertson-Walker metric and setting the scale factor a(t) equal to 1 (which reduces it to the flat-space metric of Special Relativity), we notice a null path means that a photon's motion is split evenly between motion through time and motion through space. Since the interval is invariant, once you start moving through space, you take away from your motion in time. This is why you see the clock of somebody moving with respect to yourself ticking at a slower rate than yours. (This is, of course, the logic that also clears up the famous Twin Paradox) Notice that motion through space faster than motion through time is not allowed since this would make the root of ds² negative. There's the Lorentzian signature at work for you.
Also, since the interval is fixed between any two events, this means everything moves through spacetime at the same rate - the speed of light. It's just a matter of how your motion is shared between time and space. A photon, or any massless particle, maximizes its motion through space, such that it is equal to its motion through time and, therefore, always travels along null paths. Motion through space greater than this are not allowed. Nothing can travel faster than c through space, but the combined motion through space and through time of any object is exactly the speed of light. We humans have most of our motion through time and therefore move through space very slowly compared to a photon.
This is also why we now switch to the affine parameter, λ. A photon has zero proper time, (τ = 0), since proper time vanishes along null paths. Proper time is the rate time ticks when you are at rest (ds² = -dt² = -dτ ²). A photon can find no rest, since it is always stuck moving at the speed of light, c. One can never find a reference frame, in which a photon is found at rest. Every observer, regardless of their motion, always reports finding photons to be traveling exactly at c. This essentially means a photon does not sense the passage of time. This is how we now know neutrinos have mass. Once they realized neutrinos could undergo what are called neutrino oscillations, which is a time-dependent phenomenon in the frame of the neutrino, this meant neutrinos could not travel at c and must have mass. This helped to solve the solar neutrino problem.
The equation for a null path in our simplified Robertson-Walker metric gives us:
Next, lets go to a frame that is comoving with the photon in question. This frame has 4-velocity:
You might be wondering why this vector is 4-dimensioanl. This ties back to special relativity uniting space and time. The first component is referred to as the "time-component", while the remaining three are the usual spatial components. So, space and time are united not just conceptually in SR, but even more fundamentally at the mathematical level.
Although we won't show this here, 4-velocity is always normalized by
Now that we're using λ, we can take a look at a null path. Null paths are paths of zero spacetime distance and they are the paths followed by massless particles, such as photons. Let's think about what this means. First, ds² (or ds) is called the interval and it's an invariant. Although space and time are now relative, every observer will always agree on the interval between any two events. Also, recall that space and time are on the same footing in Special Relativity. This means we must now think of motion, not just through space, but through time, as well. Sitting at your monitor reading this blog, all your motion is in the time dimension with zero motion in the spatial directions. Looking at the Robertson-Walker metric and setting the scale factor a(t) equal to 1 (which reduces it to the flat-space metric of Special Relativity), we notice a null path means that a photon's motion is split evenly between motion through time and motion through space. Since the interval is invariant, once you start moving through space, you take away from your motion in time. This is why you see the clock of somebody moving with respect to yourself ticking at a slower rate than yours. (This is, of course, the logic that also clears up the famous Twin Paradox) Notice that motion through space faster than motion through time is not allowed since this would make the root of ds² negative. There's the Lorentzian signature at work for you.
Also, since the interval is fixed between any two events, this means everything moves through spacetime at the same rate - the speed of light. It's just a matter of how your motion is shared between time and space. A photon, or any massless particle, maximizes its motion through space, such that it is equal to its motion through time and, therefore, always travels along null paths. Motion through space greater than this are not allowed. Nothing can travel faster than c through space, but the combined motion through space and through time of any object is exactly the speed of light. We humans have most of our motion through time and therefore move through space very slowly compared to a photon.
This is also why we now switch to the affine parameter, λ. A photon has zero proper time, (τ = 0), since proper time vanishes along null paths. Proper time is the rate time ticks when you are at rest (ds² = -dt² = -dτ ²). A photon can find no rest, since it is always stuck moving at the speed of light, c. One can never find a reference frame, in which a photon is found at rest. Every observer, regardless of their motion, always reports finding photons to be traveling exactly at c. This essentially means a photon does not sense the passage of time. This is how we now know neutrinos have mass. Once they realized neutrinos could undergo what are called neutrino oscillations, which is a time-dependent phenomenon in the frame of the neutrino, this meant neutrinos could not travel at c and must have mass. This helped to solve the solar neutrino problem.
The equation for a null path in our simplified Robertson-Walker metric gives us:
Next, lets go to a frame that is comoving with the photon in question. This frame has 4-velocity:
You might be wondering why this vector is 4-dimensioanl. This ties back to special relativity uniting space and time. The first component is referred to as the "time-component", while the remaining three are the usual spatial components. So, space and time are united not just conceptually in SR, but even more fundamentally at the mathematical level.
Although we won't show this here, 4-velocity is always normalized by
Let's pause one more time to see what this means. This normalization sets the magnitude of the 4-velocity. Since this is a tensor equation, if it is true in one frame, it is true in every frame. This means the 4-velocity is always fixed, which amounts to the same thing we said above. Everything moves through spacetime at the same rate. It's just a matter of how much our movement is shared between space and time, but the magnitude is always fixed.
Now, let's solve for the energy of the photon.
Next we can consider the energy of the photon emitted at scale factor a1 and time t1, and absorbed at scale factor a2 and time t2, and divide the two energies. This is exactly the second scenario we looked at above.
This amounts to the following redshift
And, there you have it!
This is a Cosmological redshift. Nowhere in this formula are relative velocities mentioned, which we would need for a Doppler Shift. Only the scale factors, which control the expansion of space, are referenced and control the redshift!
Wasn't that like totally cool? I hope, at the very least, I have provided you with plenty of ice-breakers for starting up conversations at the next party you attend. Trust me, you will be the coolest guy/gal around, if you do. ;-)
Here are the links to the professionals I promised. Reading through those will provide additional insight, but I think you'll find agreement isn't 100%. At the very least, I think you'll find this whole business of redshifts isn't as simple as it's usually made to sound in popsci.
Sean Carol's Blog
Ted Bunn's Blog I
Ted Bunn's Blog II
Well, now that I'm wrapping this blog up, I gotta admit, making all those equations was a pain in the ass at first. I think I might be getting the hang of using the LateX equation editor, which generates the images of these equations. Regardless, it is pretty obvious these physics blogs are much more work, if they're going to include math. I'll still write them up from time to time, but they probably won't be as prevalent as some of the other topics.
Have a good one!











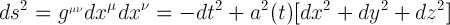


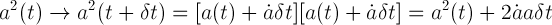










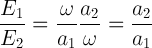

No comments:
Post a Comment