This blog post is basically a long-winded discussion about the dorky physics humor contained in the Dilbert cartoon above. Some basic calculus is used, but this post was written in the hopes that those without that background can just read around the equations and just enjoy the trippy conceptual ideas.
Seems like the term "quantum" is most often used in the phrase "quantum leap", referring to something large. In terms of Quantum Mechanics (QM), quantum refers to something very small. Specifically, it refers to the fact that energy seems to come in tiny, discrete amounts. For example, only certain electron orbits are allowed in the hydrogen atom, which correspond to distinct energy levels. A quantum "spring" is only able to vibrate at specific frequencies, which represent specific energy levels. Photons are the smallest discrete "ripple" of the electromagnetic field. The graviton would be the smallest discrete "ripple" of space time - whatever that means! And, so on. All of nature seems to have this rather surprising and mysterious property at the smallest of scales.
The scale of this discrete nature is more, or less, controlled by a constant called hbar (ℏ), which is Plank's Constant (h) divided by 2*π.
This is a very small number. On the macroscopic scale we humans reside, these energy levels appear continuous. But, if we zoomed way in, we would see their discrete nature.
In this blog post, I am going to go over the very first problem a physics student would encounter in their introductory quantum mechanics class - the particle in the infinite box, or infinite potential. It demonstrates explicitly on a mathematical level the discrete nature of different energy levels of a system. It also makes for a nice introduction to some of the strange conceptual ideas in QM.
First, let's get familiar with the infamous Schrödinger Equation!
Where
is the Laplacian (∇²), the Greek letter psi (ψ) represents the wave function, hbar (ℏ) is Planck's constant, V is the potential, m is mass and i is the usual guy from complex numbers. This is what's known as a differential equation, which contains relationships between variables and the rates of change of those variables, often with respect to time and/or space. This type of mathematical equation is used to model all sorts of behavior all throughout the sciences. The Schrödinger Equation models the behavior of the wave function.
To make things simpler, conceptually and mathematically, we'll just work in one spatial dimension, x, giving a simpler version of Schrödinger's Equation. This will also help to visualize what's conceptually going on with the particle in the infinite box. The Schrödinger's Equation reduces to the following form, with only one spatial dimension, x.
Since we're going to be using a potential V that is independent of time, we can solve this differential equation via a technique called separation of variables. I won't go into the details so that we can get to the cool ideas behind Quantum Mechanics quicker, but it leaves us with what is called the time-independent Schrödinger Equation. This is easier to work with and later we can slap on the time-dependent piece.
The basic setup for the particle in an infinite box looks like the following.
 |
We need to solve the Schrödinger equation for inside the box where the potential goes to zero. If we set the potential to zero (V=0) in the time-independent Schrödinger Equation and rearrange, we obtain the following:
This is very easily solved for psi, giving
where A and B are constants that are to be obtained by solving for the boundary conditions. This means we are going to join the solution to the outside of the well. Here the wave equation (ψ) must be equal to zero, since the particle cannot tunnel through the box, as mentioned above. Hence, for continuity, we must have
which means
so, B = 0, and hence,
Therefore,
From the properties of the periodic sine function, this means ka must satisfy the following:
for any integer, n. One can see the repeating zero values of the sine (sin) function in the following plot.
for any integer n. These are the only energy levels allowed for this system, with in between values being "forbidden".
Our wave function for the particle in a box is now in the following form.
In order to figure out how to determine the factor of A, we're going to have to introduce Born's Statistical Interpretation of the Wave Function. In the early days of quantum mechanics there was much thought put into what one should make of the wave function. Does it represent something real, or what is referred to as ontic? Or, is it just some fancy mathematical machinery that happens to give correct physical predictions, without representing anything to do with physical reality. More recently, some work has come out that strongly suggests the wave function is indeed to be regarded as something real. See this paper.
This also gets into the whole wave-particle duality idea. We normally think of waves and particles as separate entities. One is spread out in space (waves), while the other is localized in space (particles). Quantum entities on the other hand can take on the nature of both waves and particles, depending upon what's going on. A particle in the box is really a "wave-particle" in a box.
To this day, we still don't really understand what is fundamentally going on and there are multiple versions and interpretations of QM that attempt to make sense out of it all. It's all part of what's called "The Measurement Problem" in Quantum Mechanics and it's related to the mysterious nature of observation. Measurement takes a state represented by a wave function, which is spread out over many possible values, and collapses it to a specific value, or outcome. The wave function coefficients encode the probabilities of obtaining that value, or outcome. This collapse is very mysterious and not understood. Note that this means QM is a probabilistic theory, in that it does not determine definitively what a measurement will yield. Sounds very strange, I know! Hang in there and hopefully it will become a bit more clear.
A statistical interpretation of the wave function, formulated by Born, says:
Put loosely, the wave function represents a set of potentialities of what one will get upon measurement. The absolute square of the wave function (given by left side of the equation above) quantifies those probabilities (given by the right side of the equation). Before the act of measurement, the system exists as a cloud of potentialities spread out in space, or in a superposition of all potential outcomes. The act of measurement forces the system to take a stand and take on a definite outcome - in our case, the particle appears at a specific spot within the box. This is the collapse of the wave function mentioned above and is a great illustration of quantum weirdness.
A more specific example might help. Here is a simpler, generic wave function representing the spin of a particle. It has only two discrete states: spin-up and spin-down.
The absolute square of the coefficients (|a|² and |b|²) of each component of the wave function represent the probabilities of obtaining either spin-up, or spin-down, upon measurement (of course, |a|² + |b|² = 1). Before the act of measurement, the particle exists in a superposition of both the spin-up and spin-down state. A rather bad, but interesting analogy, is like trying to picture a beach ball spinning to the left and to the right, at the same time! Classical objects just do not exist in a superposition of states like this. This is apparently what reality is very much like on the quantum level, however.
Schrödinger came up with a famous thought experiment, contrasting the difference between the everyday weirdness of the quantum realm with the everyday normalcy of the classical world we're all familiar with. In this thought experiment a cat is stuck in a box with a contraption containing a radioactive isotope. There is such a small amount that over the course of an hour there is a probability of one atom decaying. If that atom decays it releases a poison contained in a vial, which would then kill the cat.
Before the experimenter looks in the box and takes a measurement, the atom exists in a superposition of decayed and not-decayed, according to the wave function for the atom. However, it seems to immediately imply the cat would also be in a superposition of being both alive and dead. However, we all know that cats are either alive OR dead, never both! What is going on? This is a clear demonstration of how the logic between the reality of the quantum world and the macroscopic world do not mesh. We still don't have a cohesive theory which meshes the two worlds, thereby solving the measurement problem, or the mystery behind the collapse of the wave function .
 |
| Schrödinger's Cat In A Simultaneous State of Being Both Alive And Dead |
Many scientists found it greatly disconcerting that we are unable to say exactly where a particle is before measurement. Some suggested that Quantum Mechanics is an incomplete theory. Therefore, the wave function did not contain all the information on the particle, which was the reason for the probabilistic predictions. Somebody would eventually find the so-called "hidden variables" and the matter would be cleared up. Needless to say, this has not happened yet and it is widely regarded that quantum particles do not contain well-defined histories like classical particles. I'm going to go into all this in more detail in a future blog post that will cover the EPR (Einstein-Podolsky-Rosen) paradox and a derivation of Bell's Theorem, as well as cover some of the interpretations of quantum mechanics. Bell's theorem basically says any local hidden-variable theory must be incompatible with Quantum Mechanics. This would mean Quantum Mechanics would have to be not only incomplete, but downright wrong. On the other hand, if Quantum Mechanics is right, then no local hidden variable theory can rescue us from certain non-local features illustrated by the EPR paradox. To this date, no experiment has shown the expected deviations in QM predictions one would expect if it were wrong and a feasible hidden variable theory was waiting to be discovered. Just a small teaser for an upcoming blog ;-)
In the meantime, the above statistical interpretation tells us how to normalize our wave function, thereby determining our unknown constant, A. The following equation says the particle has to exist somewhere, or that the probabilities of resultant outcomes upon measurement all add up to 1, or 100 percent.
By solving it, we can figure out what A is.
which means,
This finally gives us the following equation for our wave function. We have also slapped on the time-dependent piece one obtains from the separation of variable technique mentioned earlier.
The big yellow image below contains various plots of the absolute square of this wave function, which represents the probability of finding the particle in that position upon measurement. Each plot represents a different energy level. Let's look at the top row. These equations and plots are in two dimensions, x and y. The vertical axes on the plot on the left is probability. The plot on the right is just another representation of the plot on the left - the brighter, the more likely it is to find the particle in that spot upon measurement. For the ground state, or top row, we can see that we are the most likely to find the particle in the center of the box, with decreasing likelihood as we move outwards. The second row of plots is interesting. Here we see it is equally likely to find the particle on one side or the other, but there is no chance of finding it in the middle of the well. One might be wondering how does the particle travel from one side to the other, if it can never be in the middle. This is a hint of non-locality, which one encounters in QM. The particle is not located at any specific location before measurement, but is rather spread out in space, in accordance with the wave function. It's only upon measurement, that the particle takes a stand and appears at a specific location. If one performed this measurement over and over again on many identically prepared systems - called an ensemble - one would find that the outcomes would agree with the probability distributions given by the wave function.
 |
| Absolute Square of the Wave Function For the Particle in An Infinite Potential Well |
A very interesting experiment called the double-slit experiment further illustrates how a particle can be spread out in space. To put that another way, a quantum particle does not follow a defined path through space like a classical particle does. It follows all possible paths. The outcome of the double slit experiment is contingent upon the particle traveling through two slits at the same time. A seeming impossibility for a "particle" and a further demonstration of wave-particle duality. I plan to cover the double-slit experiment in yet another upcoming post, so I won't go into it anymore. However, I'll leave the following video for anybody who's dying for more quantum weirdness and doesn't want to wait.
Getting back to Dilbert's Cartoon, we can make a bit more sense out of the humor. They're simply making fun of the Quantum Mechanical notions of superposition and the mysterious act of observation.
Here's another little QM goodie. Isn't physics humor the best, hehe?




















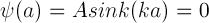












No comments:
Post a Comment